And sometimes you get unlucky. Sometimes designing a game or an experiment takes days, weeks, or months of tweaking multiple variables. It’s like flying a helicopter. Move the stick and the other controls have to be adjusted to compensate. As you panic, you and your experiment hurdle to the ground in a screaming ball of flames.

A student approached me with an interest in racial prejudice and cognitive bias. Both of these topics have been studied in great detail, and there are educational programs designed to teach students about racial stereotypes. However, to my knowledge, there aren’t any games that educate students by exposing them to their own cognitive biases. Consequently, we though it would be good idea to have students participate in a mystery game where they had to find a killer via clues and mug shots. We anticipated that players would demonstrate an in-group bias for their own race** and an out-group bias for other races. Specifically, they were expected to identify other races as the perpetrator more often than members of their own race. They were also expected to identify their own race as victims more often than other races.

We were particularly interested in an effect reported by Hilliar and Kemp (2008). In their experiment, faces were morphed between stereotypical Asian and Caucasian faces, and subjects were more likely to report these morphs as Asian when they were labeled with an Asian name rather than a European name. Unfortunately, every game mechanic we came up with introduced a confounding variable into the experiment. There is an art to identifying confounds and younger students typically lack the experience it takes to find them. As facilitators, we should weed out the confounding variables without destroying the student’s self esteem. My solution is to first notify the student that you are working in parallel on a new design. At this point, the student is already aware there are difficulties with the experiment, so the news is not too surprising. Then, take the best suggestions the student made during lab meetings and write them down. Include as many of these contributions into your design as possible. Graduate students are well accustomed to having their experimental proposals nitpicked in order to make them stronger. However, younger students often feel the war being waged on the experimental design is a personal attack. Because it is more important to keep students interested in science, I recommend keeping the academic lashings to a minimum. Show the student what the problem was, how to improve the design, and let them know their contribution was essential. You don’t want to turn into this guy.

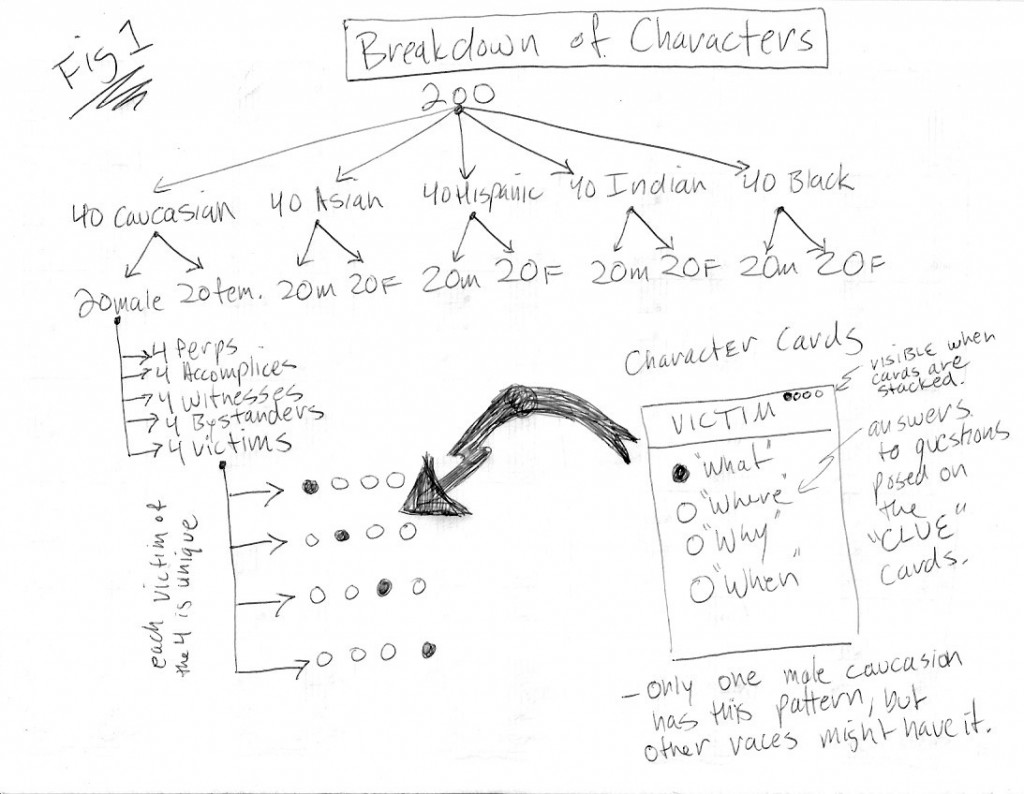
The most critical improvement in the new game was that it now relied upon a more robust experimental paradigm. Rather than using ethnic sounding names and morphed faces, players will make judgments about several faces from five major racial groups attending York College (Caucasian, Asian, Hispanic, Indian, and Black). 40 faces from each racial group will be combined to yield 200 faces (Figure 1). Within each racial group, 20 faces will be male and 20 will be female. The game is still a mystery/who-done-it, and the object of the game is to accurately identify the perpetrator, an accomplice, a witness, an innocent bystander, and the victim. Each of these characters represents an archetype associated with a particular emotional valence, ranking from negative to positive. For example, an accomplice is typically regarded as negative, but not as bad as the perpetrator. Players rank faces in the game using these characterizations similar to a Likert scale. We predict players will more likely identify members of their own race as victims, bystanders, or witness. Conversely, players are expected to identify members of other races as perpetrators or accomplices.

The core mechanic of this game is similar to Mastermind Challenge (a two-player version of the classic Mastermind), Guess Who (a pictorial variation of 20 Questions), and Clue. Like a combination of Mastermind and Guess Who, each player will attempt to identify the five characters that their opponent selected before the start of the game. Opponents are allowed to answer simple “yes-no” questions on each round of play, and players are allowed to adjust their guesses based on this feedback. However, unlike these games, players will be making judgments based on both faces and clues that are revealed on clue cards during each round of play (Figure 2). Face cards are accompanied by character cards, which indicate certain qualities about the character. After 40 rounds of play, the players guess who the five characters are, most likely revealing a racial bias.

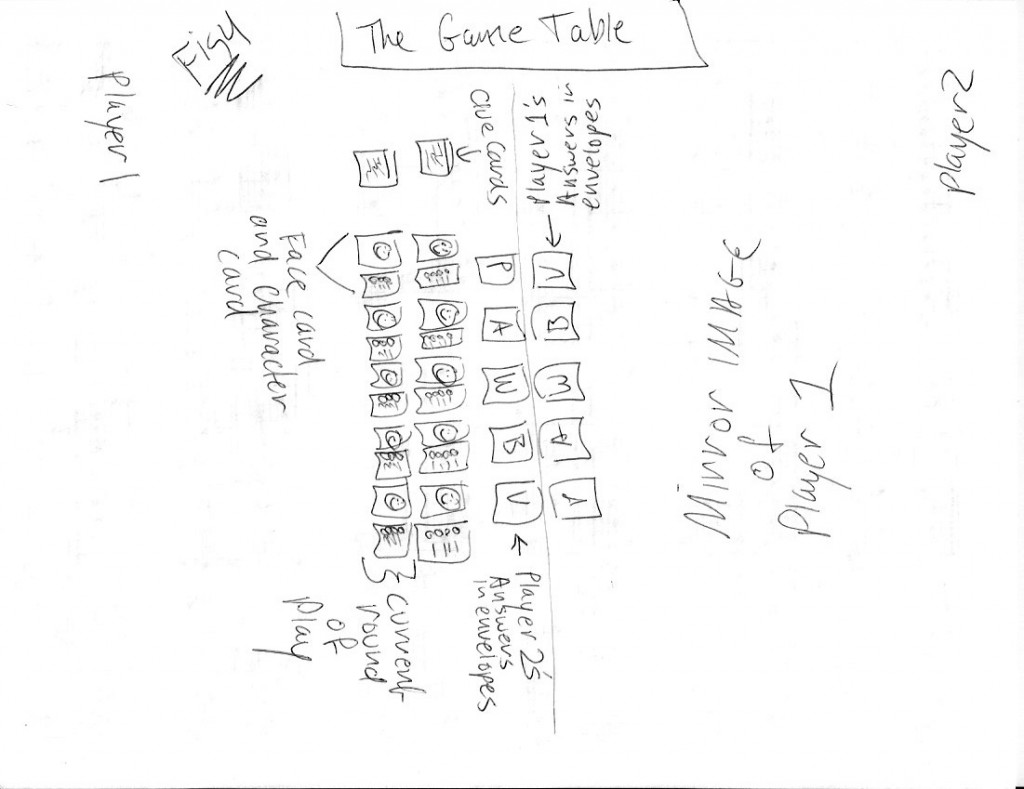
Game play commences with the reading of a story that describes the mystery. Players are told that each story comes from a real life case. Player tokens are placed on a game board and five location cards are placed on the board to make its appearance resemble locations described in the story (Figure 3). Face cards and character cards are arranged in piles (Figure 4) according to the five character categories (i.e., Perpetrator, Victim, etc.). Face cards and character cards are shuffled within each category. Players take turns picking a face-character pair for each of the five categories. These selections are noted on answer keys and placed in envelopes. For each round of play, players will roll a 4-sided die and move a token on a game board to one of the locations along the shortest path possible. Locations are spaced far enough apart so that, on average, it takes 10 turns to get from location to location. During each round of play, five face cards and five character cards are flipped over for each player to reveal the faces and character information. Then, a clue card is flipped over. Clue cards ask one “yes-no” question about a character type (e.g., Victim) using the context of the story, and that question is meant to reveal something about the character’s four traits (“what,” “where,” “why,” and “when”). For example, a question intended to reveal information about the Victim might read “Was the victim seen in his bedroom between 9pm and midnight on the night of the crime?” This question is designed to get at “when” information for the character. Character cards all have checkboxes to indicate yes or no for the four traits. If the “when” box is checked in this example, the player should conclude that the character was present during the crime, and this character might be the Victim. For each round of play, a new set of cards is revealed beneath the previous set. After the first round of play, players can switch any set of cards from one category with another set from the same category and hazard a guess. The opponent indicates whether the guess is correct with a simple “yes” or “no,” and how many are correct without revealing which ones are correct. When a player lands in one of the five locations on the board, they must Report to the Chief Inspector. During the report, they must stack all the cards from previous rounds of play, making them inaccessible for swapping. Statistically, this should happen about every 10 rounds of play, and thus players will do this four times during the game. The final guess is made after 40 rounds of play and after the player has visited the final location. If you’re still reading this, welcome to the flaming helicopter crash that is experimental game design.

While the game could be played only with character cards, the inclusion of face cards allow us to expose the player’s bias. While each character within a race-gender classification has a unique character card, there may be characters from other races or genders with a similar card. Eventually, players have to start making judgments about faces in addition to character traits, and that is how we intend to expose racial bias. While judgements of character cards are explicit, judgments of face cards are implicit. The distribution of faces, clues, and character traits had to be carefully balanced within each character category. Within each category (e.g., Perpetrator), there are 40 face cards and 40 character cards that correspond to each round of play. 20 of the faces are male. Within that group, there are four members from each of the five racial groups. Each of those four faces is paired with a unique character card.

While the experiment and the game mechanic are in far better shape, there are many things that could be improved. There are no tangible resources to manage in the game. Nevertheless, not every game requires physical resources. And managing resources might actually make it easier to keep track of the characters, thus making the game more about record keeping. Similarly, writing down clues might make the game too easy. Consequently, the one boundary that we have imposed on players is that they are not allowed to take notes. More important, however, is that the game lacks a method for controlling flow. I’m concerned that the game will either be too easy or too difficult. Only play testing will determine whether that’s the case. Finally, in writing this post, I realized that it should be possible to combine character and face cards, but I’m forgetting why I didn’t do that in the first place. Why do I have a sense of dread? What am I doing in this helicopter, and where are we going?

**I use the term “race” to indicate the socio-cultural group or ethnicity that the player identifies with.

Hilliar, K. F. and Kemp, R. I. (2008) Perception, vol. 37, pp 1605-1608.

In this post, I’ll describe the progress we’ve made on a second game for the York College summer research program. We only have six weeks to design the games, collect data, and present our results at a local conference. There might be time to shower and eat.

Sometimes you just get lucky. A student comes to you with an interest that turns into a pithy concept that’s easy to implement as a game. One of my students expressed an interest in multitasking. This issue has received a lot of attention in recent years due to the rapid proliferation of the Internet and mobile technology. Most people, particularly my college students who text during lectures, operate under the illusion that they can multitask. The illusion of multitasking is convincing because they we can accomplish more than one goal at a time by rapidly switching between tasks. People who operate under this illusion are not entirely misguided. We have an enormous capacity to process large amounts of sensory information from various modalities (e.g., sight and hearing) at the same time. And we have the ability to execute multiple motor commands at the same time (e.g., walking and chewing gum). However, we are particularly terrible at making more than one decision at a time. In attention research, this phenomenon is referred to as a “bottleneck.” As a demonstration, try to read a book while listening to the news. At some point, if you are absorbing the reading, you will miss some critical information on the news. Hal Pashler’s laboratory at UCSD has done revealing experiments on multitasking. They found that when subjects were attending to a stimulus, decisions made in response to a second stimulus were delayed until after a decision about the first stimulus was made. Our educational objective for Multitasker was to demonstrate to students that performance suffers when you attempt to multitask. We predicted that students who played the game would have a different opinion of multitasking relative to students who did not play the game.

Because we have very little time to make this game, we opted to make a board game. Another advantage of making a board game is that players can be challenged with very physical tasks, which we hope will make the lesson more evident. The core mechanic of the game revolves around trying to complete up to four tasks at the same time. A timer will be used to insure players perform each task for a sufficient period of time. We decided to adopt a few of the mini-games in Cranium (i.e., drawing and sculpting). However, some of the tasks will be modified so they can be performed simultaneously. Additionally, we might have to find tasks where the fail state is obvious. For example, it’s obvious when you drop a ball during juggling, but it might not be obvious when a person stops drawing or sculpting. Also, we are still looking for two tasks that can be accomplished with either a foot or using the voice.

To insure that players will not be overwhelmed immediately by performing four tasks at once, the number of possible tasks on any given round of play will be determined in advance in a series of levels. In level 1, the role of a four-sided die will be used to assign the one of the tasks to the player. In level 2, the role of the die, even or odd, will be used to pick two tasks. In level 3, the role of the die will be used to pick two tasks, but the player can choose the third task. In level 4, all four tasks must be performed. If a player successfully performs three challenges in a row, then they advance a level. However, if the player fails a given trial, they are moved back a level. Thus, flow is maintained by introducing and removing tasks. It’s worth noting that this method of using a 3-up/1-down staircase is standard in psychophysics. The object of the game is to be the first to complete Level 4, performing all four tasks three times in a row.

While the core mechanic of the game, objective, and reward/punishment schemes are designed, we are still looking for a fun method of providing feedback. In a previous post, I provided arguments for starting the design process with an educational objective and a game mechanic before designing the user interface. However, as I also mentioned, you can get surprising results from developing the three in parallel. Even though there are still details to complete for the game mechanic, my students also designing a toy that will serve as the centerpiece of the game. They toy will have several functions: (1) It will act as a repository for the game materials; (2) It will act as a method of keeping score and ranking the players; (3) And it will hopefully convey a message about student life. Raph Koster and Jessie Schell both indicate that user interface should be a fun toy. It’s an invitation to play, and I’m hoping my students can come up with some fun ideas that go beyond the traditional game board (a.k.a. “Game Bored”).

Now that I’ve explained our lab’s method of game development and rapid prototyping, I’m going to briefly explain the rationale for some of the games in development and describe the progress we’ve made in the past two weeks. Keep in mind that we only have six weeks to design the games, collect data, and present our results at a local conference. It’s a sprint.

Decision Maker is designed to teach students about decision-making and to help them make better decisions under uncertain conditions. Decision-making was thoroughly studied by Danniel Kahneman and Amos Tversky, who are considered the fathers of behavioral economics. Kahneman received a Nobel Prize for their work in 2002 (after the passing of Tversky in 1996). Their model of decision-making was called Prospect Theory and, in the classic paradigm, subjects must choose between a sure bet (e.g., $100) and the prospect of winning a lottery (e.g., 50% chance of winning $214). The utility of each prospect is defined as the probability multiplied by the value. In our example, the prospect would be the wisest choice because the overall utility of the bet, $107, is higher than the utility of the sure bet, which is $100.  What Kahneman and Tversky discovered, however, was that people often behaved irrationally when presented with bets that had extreme probabilities or values. The astronomical prize money and the misperception of extremely low probabilities explain why people would pay $5 for a state Lotto ticket when the odds of winning are overwhelmingly against the player. While Prospect Theory has been around for years, there have been few efforts to shape behavior given this knowledge. Merely telling people how to make decisions is not enough to alter their behavior. Consequently, Decision Maker is designed to train students to improve their decision-making skills for extreme probabilities and values.

Designing games that are fun, educational, and able to collect data for scientific purposes is challenging. After the educational objectives of our games are established, we develop experimental protocols that will allow us to assess the behavior we wish to shape. Then, we develop game mechanics that compliment those experimental protocols. Our lab uses Tracy’s Fullerton’s Game Design Workshop and Jessie Schell’s Game Design: A Book of Lenses to ensure we address the most critical elements of game design. While it’s not necessary to adhere to this particular order, I recommend starting with a good scientific experiment. However, it is sometimes useful to develop the experiment and game mechanics in separate “sandboxes.” I often ask students to simultaneously design an experiment, a game mechanic, and a fun toy/interface to play with. Combining the results of independent endeavors often produces interesting and unexpected surprises.

Fortunately for Decision Maker, there are several experimental paradigms from behavioral economics to consider. We adopted a method of adjustment paradigm where players indicate the sure bet they would accept in lieu of a given prospect. Players will be presented with positive and negative prospects, and prospects will vary widely in probability and value. The set of probabilities and values were randomly generated to make the mental computation of utility difficult (e.g., 0.2% chance of winning $10,147). Using the staircase method typically employed in psychophysical experiments, the difficulty of the decisions will increase when players make more correct decisions, and the difficulty will decrease if they make errors. The staircase allows us to find the threshold where decisions become less reliable, and it keeps players in a state of flow (where the task is optimally challenging without being too frustrating or too boring). While multiple ascending and descending staircases can be interleaved, we decided to go with a simple descending staircase with consistent step sizes between trials. Our prediction is that subjects who play our game will preform better on a post-test of decision-making relative to control subjects who received equivalent practice in decision making without using games.

After the experiment was designed, we developed the game mechanics. Some of these mechanics are more clearly defined in Tracy’s book, but I’ll briefly define them here. Objectives describe what the player is trying to achieve in the long run. They can describe intermediate goals or the ultimate win/fail states of the game. Resources are items in the game that you are either acquire or get rid of to achieve your objective (e.g., the pieces in Chess or the money in Monopoly). Feedback mechanisms are implemented in games to inform the player about their performance (e.g., point totals or badges). Reward/Punishment Contingencies describe how and at what rate the game will react to a player’s decisions. Different contingencies can have dramatically different effects on behavior. For example, more work is typically elicited from pigeons if rewards are intermittent rather than consistent. With effective contingencies and feedback mechanisms, behavior can be shaped quickly to help the player achieve their objective. Of course, games don’t always have to be friendly. Unreliable feedback mechanisms can be used to achieve a different effect. Flow has been defined in detail elsewhere. Students should focus intensely on how to use all the other mechanics and standard psychophysical procedures to elicit a state of flow in the players. The staircase method should be the starting point when considering flow. Finally, boundaries are rules that prevent players from acting in a particular way. While limiting player behavior might appear to be a fun killer, boundaries often have the opposite effect. For example, soccer is really only fun because players are not allowed to use their hands. This game mechanic is best employed when you are not making progress on a design. If a student is functionally fixed on a particular design that is not working, introduce a boundary to change the designer’s frame of reference.

The core game mechanic for Decision Maker rests on how prospects are presented to the player and how the player evaluates those prospects. Prospects will be presented on playing cards along with scenarios related to student life. Players must write down the sure bet they would accept in lieu of the prospect. The correct utility of the prospect will appear on the back of the card. Players are rewarded for correct decisions by receiving a card and they are punished by not receiving a card. The objective of the game is to accrue more cards than your opponent before the deck of cards is exhausted. After a choice is made, the player spins the dial of a spinner and watches the gamble play out in real time. It’s important to note that, just like the state Lotto, players can win on rare occasions even if the choice to gamble is incorrect. Immediate feedback is implicit when the player flips the card to see the correct answer, but feedback is also available by comparing how many cards each player has collected relative to the opponents. We didn’t really feel the need to impose boundaries in this game because the behavior is fairly controlled and we didn’t want to further limit our players. Because we are developing this game as a board game, implementing a psychophysical staircase procedure was a little trickier. We decided to introduce levels into the game. Each level will have it’s own spinner and deck of cards. During early levels, the player will evaluate relatively easy prospects (i.e., within the range of reliable decision making). If the player successfully answers a certain number of questions, they are advanced to the next level where more difficult decisions have to be made. If a player doesn’t accrue a significant number of cards at the end of a level, they must go back and replay that level. Thus, student must improve on their evaluation of difficult prospects in order to win the game. Spinners for the early levels will be marked to indicate probabilities from 1 to 100%. Spins for the advanced levels will represent extreme probabilities by requiring the player to make several spins in a row within a target zone (e.g., the bet for a 0.25% prospect pays off if the player gets the needle to land between 0 and 5 twice in a row). The physical task of spinning the spinner several times for low probabilities will hopefully reinforce the notion that it’s unwise to bet on rare outcomes! Players will keep track of their own score. Players must maximize their winnings and finish with the most number of cards to win the game. If a player finishes the game without having the largest total on their scorecard, all players purge their cards and the final level will be repeated until there is a winner.

To make the game more fun, we plan to add a number of physical tasks that also must be completed before advancing to the next level (e.g., stack all the blocks that come with the game Jenga). Players will have a limited time to complete mini-games, physical feats, or puzzles to pass to the next level. The addition of these puzzles will add variety to the game and allow players to take a break from performing mental calculations. Additionally, some game cards will introduce “windfalls” or “calamities” into the mix. Windfalls might spontaneously grant the player an extra turn, extra cards, or allow them to circumvent the physical task. Calamities might require the player to loose a turn, give up cards, or move back a level. To maintain balance between competitors, players with fewer cards are more susceptible to windfalls and players with more cards are more susceptible to calamities.

Our plan is to have a working prototype of this game in the next week and play test all our games so that we can collect data the following week. Subsequent posts will describe our other games and the progress made in this game.